Решение индивидуального задания «Дискретные случайные величины», Вариант 2, ПГТУ
ПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Индивидуальное задание
«Дискретные случайные величины»
Вариант № 2
1. Найти у
| Х | 1 | 2 | 5 | 6 |
| Р | 0,2 | 0,1 | 0,6 | y |
2. X и Y – независимы. D(X)=7, D(Y)=4. Используя свойства дисперсии, найдите D(2X+3Y).
3. Производится три независимых опыта, в каждом из которых может произойти событие А с вероятностью 0,4. Вычислить таблицу для случайной величины Х – числа появлений события А. Найти M(X), D(X), σ(X), m3 и F(x).
4. Игральный кубик брошен один раз. Найти закон распределения случайной величины Х – числа выпавших очков. Найти M(X), D(X), q1, функцию распределения. Построить график F(x).
5. Охотник, имеющий 4 патрона, стреляет в цель до первого попадания (или пока не израсходует патроны). Найти математическое ожидание и дисперсию числа израсходованных патронов, если вероятность попадания при каждом выстреле равна 0,25.
6. Найти M(X), D(X), функцию распределения дискретной случайной величины, заданной таблицей:
| Х | 10 | 15 | 20 | 25 | 30 |
| Р | 0,3 | 0,1 | 0,3 | 0,2 | 0,1 |
Уменьшенную копию первой страницы решения можно посмотреть ниже:
Индивидуальное задание «Дискретные случайные величины»
Решение 6 задач
Вариант № 2
Полный список решенных вариантов индивидуального задания «Дискретные случайные величины», ПГТУ вы можете посмотреть тут.
МатМозг 29 ноября, 2024
Posted In: Дискретные случайные величины, Индивидуальное задание, Математика, ПГНИУ (ПГТУ, ПНИПУ), Платные работы, Теория вероятности
Метки: Вариант 2
Решение индивидуального задания «Дискретные случайные величины», Вариант 7, ПГТУ
ПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Индивидуальное задание
«Дискретные случайные величины»
Вариант № 7
1. Найти у
| Х | -3 | -2 | -1 | 1 | 2 | 3 |
| Р | 0,1 | 0,2 | у | 0,2 | 0,2 | 0,1 |
2. M(X)=6, M(Y)=5. Используя свойства математического ожидания, найдите M(2X+3Y).
3. Вероятность попадания в мишень для данного стрелка равна 0,8. За каждое попадание стрелку защитываются 5 очков. Составить таблицу распределения дискретной случайной величины Х – числа выбитых очков при трех выстрелах. Найти M(X), D(X), построить F(x).
4. В коробке 6 теннисных мячей, из которых два окрашенных. Наудачу достают два мяча. Составить закон распределения случайной величины Х – числа окрашенных мячей, попавших в выборку. Найти M(X), D(X), σ(X), F(x).
5. Рабочий обслуживает 4 станка. Вероятность того, что в течение часа станок не потребует внимания рабочего, равна для первого – 0,9, для второго – 0,8, для третьего – 0,75, для четвертого – 0,7. Найти математическое ожидание и дисперсию числа станков, которые не потребуют внимания рабочего в течение часа.
6. По таблице распределения Х:
| Х | -1 | 0 | 1 | 3 | 5 |
| Р | 0,1 | 0,2 | 0,2 | 0,3 | 0,2 |
Найти M(X), D(X), q1. Найти P(X≥2).
Уменьшенную копию первой страницы решения можно посмотреть ниже:
Индивидуальное задание «Дискретные случайные величины»
Содержит решение шести задач
Вариант № 7
Полный список решенных вариантов индивидуального задания «Дискретные случайные величины», ПГТУ вы можете посмотреть тут.
МатМозг 15 сентября, 2022
Posted In: Дискретные случайные величины, Индивидуальное задание, Математика, ПГНИУ (ПГТУ, ПНИПУ), Платные работы, Теория вероятности
Метки: Вариант 7
Решение индивидуального задания «Непрерывные и случайные величины», ПГТУ, Вариант 23
ПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Индивидуальное задание
«Непрерывные и случайные величины»
Вариант № 23
Уменьшенную копию первой страницы решения можно посмотреть ниже:
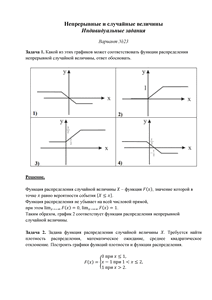
Индивидуальное задание «Непрерывные и случайные величины»
Решение содержит 6 задач
Вариант № 23
Полный список решенных вариантов индивидуального задания «Непрерывные и случайные величины», ПГТУ вы можете посмотреть тут.
МатМозг 28 марта, 2022
Posted In: Индивидуальное задание, Математика, Непрерывные и случайные величины, ПГНИУ (ПГТУ, ПНИПУ), Платные работы, Теория вероятности
Метки: Вариант 23
Решебник индивидуального задания «Непрерывные и случайные величины», ПГТУ
ПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Индивидуальное задание
«Непрерывные и случайные величины»
6 задач
Список решенных вариантов индивидуального задания «Непрерывные и случайные величины» вы можете посмотреть ниже:
МатМозг 28 марта, 2022
Posted In: Индивидуальное задание, Математика, Непрерывные и случайные величины, ПГНИУ (ПГТУ, ПНИПУ), Платные работы, Теория вероятности
Решение индивидуального задания «Теория вероятностей», Вариант 20, ПГТУ
ПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Индивидуальные задания
«Теория вероятностей»
Вариант №20
Уменьшенную копию первой и последней страниц решения можно посмотреть ниже:
Индивидуальное задание «Теория вероятностей»
Вариант № 20
1. Ребенок играет с четырьмя буквами разрезной азбуки А, А, М, М. Какова вероятность того, что при случайном расположении букв в ряд он получит слово «МАМА»?
2. Три предмета распределяются по 5 ячейкам случайным образом. Найти вероятность того, что все они попадут в разные ячейки.
3. Стержень длиной наудачу разломан на З части. Найдите вероятность того, что длина каждой части окажется больше .
4. Имеется пять билетов стоимостью по одному рублю, три билета по три рубля и два билета по пять рублей. Наугад берутся три билета. Определить вероятность того, что
а) все три билета стоят вместе семь рублей,
б) все три билета стоимостью по одному рублю.
5. Студент из 15 вопросов знает ответы только на 7 вопросов. Определить вероятность того, что из 5 наугад выбранных вопросов он знает ответы на 3 вопроса.
6. Экзаменационный билет содержит три вопроса. Вероятность того, что студент ответит на любой вопрос билета, равна 0,9. Найти вероятность того, что студент сдаст экзамен, если для этого необходимо ответить хотя бы на два вопроса билета.
7. Рабочий обслуживает три станка, вероятность того, что в течение часа для первого станка не потребуется помощь рабочего равна 0,9, для второго – 0,8, для третьего – 0,7. Найти вероятность того, что, по крайней мере, для двух станков не потребуется помощь рабочего.
8. В каждой из двух урн по 6 черных и 4 белых шара. Из первой урны наудачу извлекли шар и переложили во вторую. Найти вероятность того, что взятый после этого наудачу шар из первой урны окажется белым.
9. В урне находится один шар, о котором известно, что он либо белый, либо черный. В урну положили белый шар, а потом после тщательного перемешивания вынули наудачу один шар, который оказался белым. Какова вероятность того, что после этого вынут из урны белый шар?
10. Вероятность попадания в мишень хотя бы один раз при двух выстрелах для данного стрелка равна 0,99. Найти вероятность попадания в мишень данным стрелком при одном выстреле.
11. Вероятность появления события в одном испытании равна 0,8. Сколько нужно произвести испытаний, чтобы с вероятностью 0,95 можно было ожидать отклонение относительной частоты появления события от его вероятности не более, чем на 0,05.
12. Вероятность появления события в одном опыте равна 0,9. Произведено 900 опытов. Найти наивероятнейшее число появлений события и вероятность такого результата.
13. Определить вероятность разрыва цепи, если Pi – надежность i – го элемента
Полный список решенных вариантов индивидуального задания «Теория вероятностей», ПГТУ вы можете посмотреть тут.
МатМозг 22 октября, 2021
Posted In: Индивидуальное задание, Математика, ПГНИУ (ПГТУ, ПНИПУ), Платные работы, Теория вероятности
Метки: Вариант 20
Решение расчетного задания по теме «Случайные события», Вариант 6, ПГТУ
ПГТУ
Расчетное задание по теме
«Случайные события»
Вариант 6
1. На полке наугад расставлены 18 книг. Найти вероятность того, что:
а) три тома одного сочинения окажутся поставленными вместе в порядке номеров;
б) три тома будут поставлены вместе.
2. Вероятность отказа за время Т для первого элемента равна 0,1; для второго – 0,2; для третьего – 0,15. Найти вероятность безотказной работы цепи за время Т. Схема включения элементов цепи приведена на рисунке:
3. На сборку поступило 3 000 деталей с первого автомата и 2 000 со второго. Первый автомат дает 0,27 % брака, а второй – 0,33 %. Найти вероятность попадания на сборку бракованной детали, если деталь выбирается наудачу из всех деталей. Найти вероятность того, что взятая наудачу деталь изготовлена первым автоматом, если при проверке она оказалась стандартной.
4. Производится 6 выстрелов по цели. Вероятность попадания при каждом выстреле равна 0,7. Найти вероятность того, что:
а) произойдет одно попадание в цель;
б) произойдет не менее пяти попаданий;
в) произойдет хотя бы одно попадание.
Уменьшенную копию первой страницы решения можно посмотреть ниже:
Вариант 6
Список решенных вариантов данного расчетного задания вы можете посмотреть тут.
МатМозг 12 апреля, 2020
Posted In: Математика, ПГНИУ (ПГТУ, ПНИПУ), Платные работы, Расчетное задание, Теория вероятности
Метки: Вариант 6
АГУ (16)
АлтГТУ (2)
БГАТУ (14)
БГАУ (1)
БИТИ (БИТТиУ) (135)
ВГАУ (3)
ВЗФЭИ (3)
ВоГУ (93)
ВолГАУ (8)
ВятГУ (4)
ДВГТУ (41)
ДВГУПС (34)
ЗабГУ (12)
ЗКАТУ (5)
ИжГТУ (1)
ИРНИТУ (15)
КамчатГТУ (6)
КГПУ (4)
КГСХА (4)
КГУ им. Н. А. Некрасова (7)
КНИТУ (КАИ) (1)
КНИТУ (КХТИ) (1)
КубГТУ (23)
МАДИ (32)
МАИ (3)
МГГУ (16)
МГОУ (8)
МГСУ МИСИ (30)
МГТУ им. Г.И.Носова (4)
МГТУ им. Н.Э. Баумана (37)
МГТУ МАМИ (6)
МГТУ МИРЭА (494)
МГУ им. адм. Г.И. Невельского (23)
МГУИЭ (1)
МГУПИ (120)
МИИТ (152)
МИСиС (2)
МИЭЭ (18)
МТУСИ (4)
НГАВТ (41)
НГТУ (2)
НИИ (16)
НИУ ВШЭ (1)
НИУ МЭИ (105)
НИУ МЭИ (филиал) в г. Волжском (5)
НТИ (филиал) МГУДТ (6)
НЧОУ ВПО ЮСИЭПИИ (25)
ПГНИУ (ПГТУ, ПНИПУ) (567)
ПГУ (ПензГТУ) (25)
ПГУ им. Т.Г. Шевченко (1)
ПГУПС (2)
РГАТУ (1)
РГППУ (16)
РГРТУ (1)
РГУНиГ (68)
РУДН (1)
СамГТУ (1)
СВФУ (174)
СГТУ (183)
СибГУТИ (10)
СПб ГАСУ (15)
СПб ГУТ (1)
СПбГПУ (46)
СПбГУКиТ (7)
СПбГЭТУ «ЛЭТИ» (9)
СПГГИ (16)
СТИ НИТУ «МИСиС» (96)
ТвГТУ (1)
ТПУ (4)
ТУСУР (30)
ТюмГНГУ (261)
УАД (1)
УрФУ (1)
ЮЗГУ (31)
ЮУрГУ (3)
ЮУТУ (2)
