Зачёт.Ru
База готовых студенческих работ
Решебник типового расчета, Алгебра и геометрия, 1 семестр для студентов очной формы обучения институтов ИТ и РТС, Физико-технологического института, МИРЭА
МОСКОВСКИЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
АЛГЕБРА И ГЕОМЕТРИЯ
1 семестр
Для студентов очной формы обучения институтов ИТ и РТС, Физико-технологического института
Типовой расчёт
Список решенных вариантов данного типового расчёта вы можете посмотреть ниже:
Задание:
Задачи по теме «Алгебра матриц. Системы линейных уравнений»
Задача 2.1. Вычислить определитель матрицы.
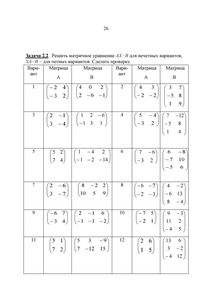
Задача 2.2. Решить матричное уравнение AX=B для нечетных вариантов,
XA=B – для четных вариантов. Сделать проверку.
Задача 2.3. Проверить совместность системы уравнений и, в случае совместности, решить ее двумя методами:
a) по формулам Крамера;
b) с помощью обратной матрицы (при нахождении обратной матрицы проверка обязательна).
Задача 2.4. Решить неоднородную систему линейных уравнений методом Гаусса. Выделить общее решение однородной системы и частное решение неоднородной системы. Сделать проверку.
Задачи по теме «Векторы. Скалярное, векторное, смешанное произведение векторов»
Задача 2.5. Даны векторы a, b, c.
1) Проверить на коллинеарность и ортогональность два вектора, указанные в столбце 1.1.
2) Проверить, будут ли компланарны три вектора, указанные в столбце 1.2.
Задача 2.6. Доказать, что векторы a, b, c, образуют базис в пространстве V3 . Найти координаты вектора d в этом базисе.
Задача 2.7. Даны координаты вершин пирамиды ABCD.
Найти:
1) внутренний угол А треугольника АВС;
2) площадь треугольника АВС;
3) объем пирамиды ABCD;
4) длину высоты, опущенной из вершины D пирамиды ABCD.
Задача 2.8.* Пользуясь свойствами скалярного и векторного произведений, вы-числить угол между векторами a и b и площадь параллелограмма, построенного на этих векторах. Угол между векторами p и q равен α.
(Задача не является обязательной. Вводится в типовой расчет по усмотрению преподавателя).
Задачи по теме «Прямая и плоскость»
Задача 2.9. Даны вершины треугольника А, В, C на плоскости.
Найти:
1) каноническое уравнение прямой АВ;
2) уравнение высоты CН (общее и с угловым коэффициентом);
3) параметрическое уравнение медианы AM;
4) координаты точки N пересечения медианы AM и высоты СH;
5) длину высоты СН;
6) координаты точки К пересечения медиан треугольника АВС.
Задача 2.10. Для точек A,B,C,D из задачи 2.7 составить уравнение:
1) плоскости AВС;
2) высоты, опущенной из вершины D пирамиды АВСD;
3) плоскости, проходящей через точку D, перпендикулярно прямой АВ.
Для точек A,B,C,D из задачи 2.7 вычислить:
4) синус угла между прямой AD и плоскостью АВС;
5) косинус угла между плоскостью ABC и координатной плоскостью XOY;
6) косинус угла между прямыми AВ и AD.
Задача 2.11*. Найти
— для нечетных вариантов: проекцию точки M на прямую L, расстояние от точки M до прямой L, точку N, симметричную точке M относительно прямой;
— для четных вариантов : проекцию точки M на плоскость P,расстояние от точки M до плоскости P, точку N, симметричную точке M относительно плоскости P .
Задачи по теме «Кривые и поверхности второго порядка»
Задача № 2.12. Составить канонические уравнения кривых второго порядка, сделать чертеж. Для случая эллипса заданы: F — фокус, α — большая полуось, b- малая полуось. Для случая гиперболы заданы: F — фокус, α — действительная полуось, b — мнимая полуось. Для случая параболы: вершина параболы находится в точке O(0,0), D — директриса, заданная указанным уравнением.
Задача № 2.13. Определить тип поверхности второго порядка, заданной уравнением. Привести уравнение поверхности к каноническому виду. Сделать чертеж. Найти сечение поверхности заданной плоскостью.
МатМозг 30 июля, 2019
Posted In: Алгебра, Геометрия, Линейная алгебра, Математика, МГТУ МИРЭА, Платные работы, Типовой расчет