Зачёт.Ru
База готовых студенческих работ
Список решебников МГУПИ
РГР №1 по Электротехнике «Электрические цепи постоянного тока»
https://www.zachet.ru/reshebnik-rgr-1-po-elektrotehnike-elektricheskie-tsepi-postoyannogo-toka-mgupi/
РГР №2 по Электротехнике «Электрические цепи однофазного синусоидального тока»
https://www.zachet.ru/reshebnik-rgr-2-po-elektrotehnike-elektricheskie-tsepi-odnofaznogo-sinusoidalnogo-toka-mgupi/
Решебник работы по теории вероятности и математической статистике
https://www.zachet.ru/reshebnik-mgupi-teorver-matstat/
Максим 5 февраля, 2018
Posted In: МГУПИ, Платные работы
Решение РГР №2 по Электротехнике «Электрические цепи однофазного синусоидального тока», МГУПИ, Вариант 96
МГУПИ
Расчетно-графическая работа №2
«Электрические цепи однофазного синусоидального тока»
Вариант 96
Схема 1.4
Уменьшенную копию первой и последней страницы решения можно посмотреть ниже:
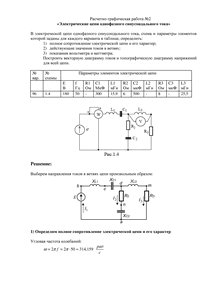
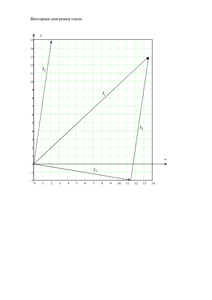
Расчетно-графическая работа №2
«Электрические цепи однофазного синусоидального тока»
Вариант 96
Схема 1.4
Список решенных вариантов РГР №2 по Электротехнике «Электрические цепи однофазного синусоидального тока», МГУПИ вы можете посмотреть тут.
Максим 26 декабря, 2022
Posted In: Линейные электрические цепи переменного тока, МГУПИ, Платные работы, РГР, ТОЭ
Метки: Вариант 96, Схема 1.4
Решение РГР №2 по Электротехнике «Электрические цепи однофазного синусоидального тока», МГУПИ, Вариант 95
МГУПИ
Расчетно-графическая работа №2
«Электрические цепи однофазного синусоидального тока»
Вариант 95
Схема 1.5
Уменьшенную копию первой и последней страницы решения можно посмотреть ниже:
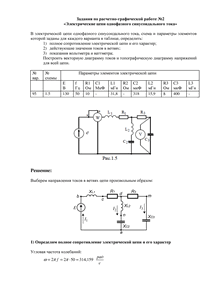
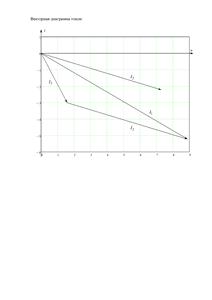
Расчетно-графическая работа №2
«Электрические цепи однофазного синусоидального тока»
Вариант 95
Схема 1.5
Список решенных вариантов РГР №2 по Электротехнике «Электрические цепи однофазного синусоидального тока», МГУПИ вы можете посмотреть тут.
Максим 13 декабря, 2022
Posted In: Линейные электрические цепи переменного тока, МГУПИ, Платные работы, РГР, ТОЭ
Метки: Вариант 95, Схема 1.5
Решение РГР №2 по Электротехнике «Электрические цепи однофазного синусоидального тока», МГУПИ, Вариант 78
МГУПИ
Расчетно-графическая работа №2
«Электрические цепи однофазного синусоидального тока»
Вариант 78
Схема 1.15
Уменьшенную копию первой и последней страницы решения можно посмотреть ниже:
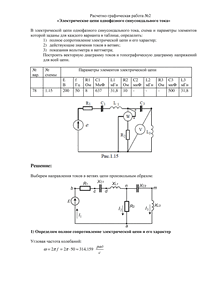
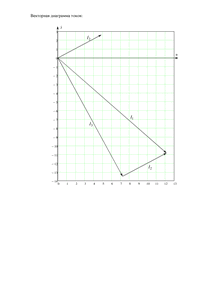
Расчетно-графическая работа №2
«Электрические цепи однофазного синусоидального тока»
Вариант 78
Схема 1.15
Список решенных вариантов РГР №2 по Электротехнике «Электрические цепи однофазного синусоидального тока», МГУПИ вы можете посмотреть тут.
Максим 22 ноября, 2022
Posted In: Линейные электрические цепи переменного тока, МГУПИ, Платные работы, РГР, ТОЭ
Метки: Вариант 78, Схема 1.15
Решение РГР №2 по Электротехнике «Электрические цепи однофазного синусоидального тока», МГУПИ, Вариант 51
МГУПИ
Расчетно-графическая работа №2
«Электрические цепи однофазного синусоидального тока»
Вариант 51
Схема 1.2
Уменьшенную копию первой и последней страницы решения можно посмотреть ниже:
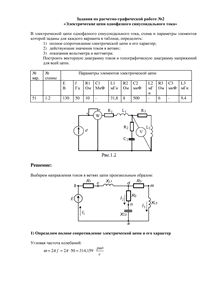
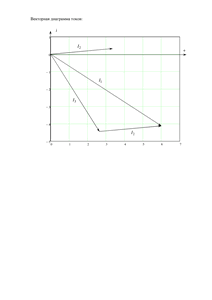
Расчетно-графическая работа №2
«Электрические цепи однофазного синусоидального тока»
Вариант 51
Схема 1.2
Список решенных вариантов РГР №2 по Электротехнике «Электрические цепи однофазного синусоидального тока», МГУПИ вы можете посмотреть тут.
Максим 2 ноября, 2022
Posted In: Линейные электрические цепи переменного тока, МГУПИ, Платные работы, РГР, ТОЭ
Метки: Вариант 51, Схема 1.2
Решение РГР №1 по Электротехнике «Электрические цепи постоянного тока», МГУПИ, Вариант 51
МГУПИ
Контрольно-графическая работа №1
«Электрические цепи постоянного тока»
Вариант 51
Схема 1.13
Положение выключателя — Разомкнут
Метод анализа — Узловых Напряжений
Уменьшенную копию первой страницы решения можно посмотреть ниже:
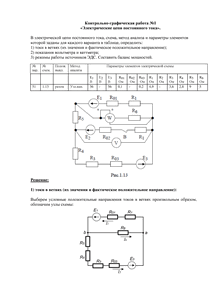
Контрольно-графическая работа №1
«Электрические цепи постоянного тока»
Вариант 51
Рисунок 1.13
Положение выключателя – Разомкнут
Метод анализа – Узл. нап.
Список решенных вариантов РГР №1 по Электротехнике «Электрические цепи постоянного тока», МГУПИ вы можете посмотреть тут.
Максим 1 ноября, 2022
Posted In: Линейные электрические цепи постоянного тока, МГУПИ, Платные работы, РГР, ТОЭ
Метки: Вариант 51, Схема 1.13
Решение РГР №2 по Электротехнике «Электрические цепи однофазного синусоидального тока», МГУПИ, Вариант 50
МГУПИ
Расчетно-графическая работа №2
«Электрические цепи однофазного синусоидального тока»
Вариант 50
Схема 1.1
Уменьшенную копию первой и последней страницы решения можно посмотреть ниже:
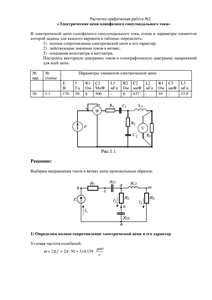
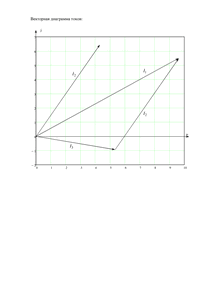
Расчетно-графическая работа №2
«Электрические цепи однофазного синусоидального тока»
Вариант 50
Схема 1.1
Список решенных вариантов РГР №2 по Электротехнике «Электрические цепи однофазного синусоидального тока», МГУПИ вы можете посмотреть тут.
Максим 30 октября, 2022
Posted In: Линейные электрические цепи переменного тока, МГУПИ, Платные работы, РГР, ТОЭ
Метки: Вариант 50, Схема 1.1