Решебник типового расчета по Математическому Анализу, II семестр, ВМС и Кибернетика, МГТУ МИРЭА

МИРЭА

МАТЕМАТИЧЕСКИЙ АНАЛИЗ
II семестр
ОСНОВЫ ДИСКРЕТНОЙ МАТЕМАТИКИ

Контрольные задания для студентов факультетов ВМС и Кибернетики

Список решенных вариантов данного контрольного задания вы можете посмотреть ниже:

Задание:

Задача 1. Найти неопределенный интеграл. По усмотрению преподавателя выполняется либо одно из заданий (а или б), либо оба задания.
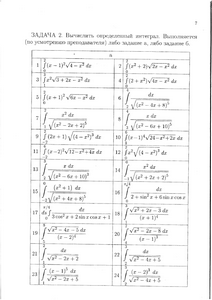
Задача 2. Вычислить определенный интеграл. Выполняется (по усмотрению преподавателя) либо задание а, либо задание б.
Задача 3. Исследовать на сходимость несобственный интеграл и вычислить его, если он сходится.
Задача 4. Изменить в двойном интеграле $\int\limits_{a}^{b}dx\int\limits_{\varphi(x)}^{\psi(x)}f(x,y)dy$ порядок интегрирования. Сделать чертеж области интегрирования.
Задача 5. Вычислить объем тела с помощью тройного интеграла, переходя к цилиндрическим или сферическим координатам.
Задача 6. Вычислить циркуляцию плоского векторного поля $\oint_{L}^{ } P(x,y)dx+Q(x,y)dy$ двумя способами: непосредственно и по формуле Грина.
Задача 7. Ниже r=xi+yj+zk, $|r|=\sqrt{x^{2}+y^{2}+z^{2}}$ , c — постоянный вектор.
Задача 8. Вычислить площадь части поверхности σ, заключенную внутри цилиндрической поверхности Ц.
Задача 9. Найти поток векторного поля а через замкнутую поверхность σ, двумя способами: 1) непосредственно, вычисляя потоки через все гладкие кучки поверхности σ; 2) по теореме Остроградского-Гаусса.
Задача 10. Найти циркуляцию векторного поля а по контуру Г, двумя способами: 1) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; 2) по теореме Стокса.

МатМозг 27 мая, 2016

Posted In: Матанализ, Математика, МГТУ МИРЭА, Платные работы, Типовой расчет

Вариант 1	Вариант 2	Вариант 3	Вариант 4	Вариант 5	Вариант 6	Вариант 7	Вариант 8	Вариант 9	Вариант 10
Вариант 11	Вариант 12	Вариант 13	Вариант 14	Вариант 15	Вариант 16	Вариант 17	Вариант 18	Вариант 19	Вариант 20
Вариант 21	Вариант 22	Вариант 23	Вариант 24	Вариант 25	Вариант 26	Вариант 27	Вариант 28	Вариант 29	Вариант 30