Зачёт.Ru
База готовых студенческих работ
А.А.Яблонский, Д1, Вариант 2
Раздел: Динамика материальной точки
Задание Д1. Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил
Вариант 2
Гавриш 23 января, 2016
Posted In: Динамика, Динамика материальной точки, Задача, Пример решения, ТерМех, ТерМех, А.А. Яблонский
Задача 176, Гмурман В.Е.
Глава четвертая. Дискретные случайные величины
§ 1. Закон распределения вероятностей дискретной случайной величины. Законы биномиальный и Пуассона
Задача 176 про тираж учебников.
Ссылка на задачник ООО «Издательство Юрайт»
http://urait.ru/catalog/387430/
Решение:
В задании дано k=5, n=100000, р=0,0001. События того, что учебники сброшюрованы неверно, независимы, n велико, вероятность р мала, значит мы можем использовать распределение Пуассона:
Pn(k)=λke-λ/k!
Ищем λ:
λ=np=100000·0,0001=10
Находим вероятность, что тираж содержит 5 плохих книг:
P100 000(5)=105·e-10/5!=105·e-10/120≈0,0378
Полный список решенных задач из руководства к решению задач по теории вероятностей и математической статистике, В.Е.Гмурман вы можете посмотреть тут.
МатМозг 15 января, 2016
Posted In: Задача, Математика, Пример решения, Руководство к решению задач по теории вероятностей и математической статистике, Гмурман В.Е., Теория вероятности
Задача № 43 по ТАУ, В.А. Бесекерский
43. Преобразовать динамическое звено, описываемое дифференциальным уравнением
во встречно-параллельное (с обратной связью) соединение консервативного и идеального дифференцирующего звеньев.
Максим 4 января, 2016
Posted In: 1. Дифференциальные уравнения и передаточные функции звеньев и автоматических систем, 4. Структурные схемы и их преобразование, Задача, Пример решения, Сборник задач по теории автоматического регулирования и управления под редакцией В.А.Бесекерского, ТАУ
Задача № 25 по ТАУ, В.А. Бесекерский
25. Какое динамическое звено имеет функцию веса w(t)=50(e-5t-e-10t)∙1(t) ? Найти параметры этого звена и записать выражение передаточной функции.
Решение:
Максим 3 января, 2016
Posted In: 1. Дифференциальные уравнения и передаточные функции звеньев и автоматических систем, 2. Типовые динамические звенья, Задача, Пример решения, Сборник задач по теории автоматического регулирования и управления под редакцией В.А.Бесекерского, ТАУ
Задача № 12 по ТАУ, В.А. Бесекерский
12. Найти передаточную функцию пружины и демпфера (рис. 9), если пренебречь влиянием массы подвижных частей и принять за входную величину силу F, а за выходную – перемещение точки A (поршня) x.
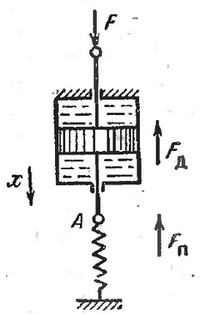
Рис. 9. Поршень с цилиндром и пружиной
Максим 1 января, 2016
Posted In: 1. Дифференциальные уравнения и передаточные функции звеньев, 1. Дифференциальные уравнения и передаточные функции звеньев и автоматических систем, Задача, Пример решения, Сборник задач по теории автоматического регулирования и управления под редакцией В.А.Бесекерского, ТАУ
Задача № 24 по ТАУ, В.А. Бесекерский
24. Найти дифференциальное уравнение и передаточную функцию центробежного измерителя угловой скорости (ЦИС) на рис. 15, а, если принять за выходную величину перемещение муфты x, а за входную – приращение угловой скорости ∆Ω и считать известными приведенную к точке M массу всех шаров m; длины рычагов l1, l2, l3; приведенные в точке B муфты а) силу пружины FП, б) силу вязкого трения и демпфера FД, в) инерционные силы приведенных масс FИ и г) приведенные силы от веса всех подвижных частей FВ. Влиянием сил сухого трения пренебречь.
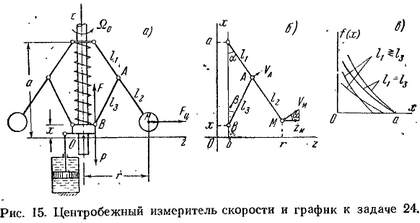
Максим 1 января, 2016
Posted In: 1. Дифференциальные уравнения и передаточные функции звеньев, 1. Дифференциальные уравнения и передаточные функции звеньев и автоматических систем, Задача, Пример решения, Сборник задач по теории автоматического регулирования и управления под редакцией В.А.Бесекерского, ТАУ