2. Критерий устойчивости Михайлова

123. Система автоматического управления имеет характеристический полином 6 порядка. На рис. 81 приведены кривые Михайлова для различных значений параметров системы. Определить устойчивость системы

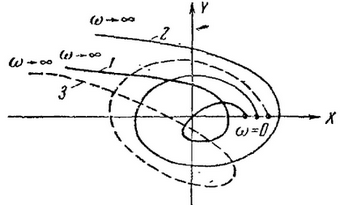
Рис. 81. Кривые Михайлова к задаче 123

Рис. 81. Кривые Михайлова к задаче 123

Уменьшенную копию первой страницы решения можно посмотреть ниже:

Решение задачи № 123
из СБОРНИКА ЗАДАЧ ПО ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И УПРАВЛЕНИЯ
Под редакцией В.А. Бесекерского

Оплатить 220.⁰⁰ RUB

Полный список решенных задач из сборника задач по теории автоматического регулирования и управления, В.А. Бесекерский вы можете посмотреть тут.

Сергей 23 апреля, 2020

Posted In: 2. Критерий устойчивости Михайлова, 3. Устойчивость линейных систем, Задача, Платные работы, Сборник задач по теории автоматического регулирования и управления под редакцией В.А.Бесекерского, ТАУ

Метки: Рисунок 81

134. Характеристический многочлен автоматической системы равен

$\displaystyle D(p)=2\cdot 10^{-4}\cdot p^{6}+80\cdot 10^{-4}\cdot p^{5}+$

$\displaystyle +2\cdot 10^{-1}\cdot p^{4}+1,24p^{3}+10p^{2}+40p+34$

Определить устойчивость системы.

Уменьшенную копию первой страницы решения можно посмотреть ниже:

Решение задачи № 134
из СБОРНИКА ЗАДАЧ ПО ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И УПРАВЛЕНИЯ
Под редакцией В.А. Бесекерского

Оплатить 220.⁰⁰ RUB

Сергей 22 мая, 2018

125. На рис. 83 приведена кривая Михайлова автоматической системы, имеющей характеристическое уравнение пятого порядка. Нарисовать качественную картину расположения корней характеристического уравнения на плоскости корней.

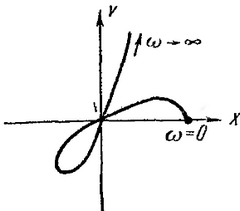
Рис. 83. Кривая Михайлова к задаче 125.

Решение:
Уменьшенную копию первой страницы решения можно посмотреть ниже:

Решение задачи № 125
из СБОРНИКА ЗАДАЧ ПО ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И УПРАВЛЕНИЯ
Под редакцией В.А. Бесекерского

Формат файла PDF (в архиве ZIP)

Оплатить 220.⁰⁰ RUB

Сергей 6 января, 2016

Условие:
Структурная схема автоматической системы приведена на рисунке. Общий коэффициент усиления разомкнутой системы K=k₁k₂k₃k₄=10; постоянные времени T=0,2 c, T₀=0,8 c. Используя критерий устойчивости Михайлова, определить величину постоянной времени корректирующего устройства τ=τ_k, при которой система находится на границе устойчивости.

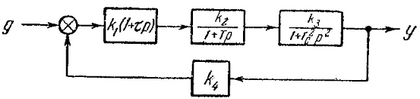
Структурная схема системы к задаче 130

Рисунок. Структурная схема автоматической системы.

Решение:
Уменьшенную копию первой cтраницы содержимого можно посмотреть ниже:

Решение задачи № 130
из СБОРНИКА ЗАДАЧ ПО ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И УПРАВЛЕНИЯ
Под редакцией В.А. Бесекерского

Формат файла PDF (в архиве ZIP)

Оплатить 220.⁰⁰ RUB

Список решенных задач из задачника по ТАУ, В.А.Бесекерского вы можете посмотреть тут.

Максим 27 июля, 2015

Условие:
Система автоматического управления имеет характеристическое уравнение 4-го порядка. Кривая Михайлова системы изображена на рисунке. Определить устойчивость автоматической системы.

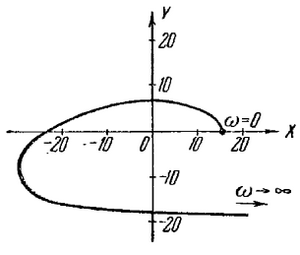
Годограф Михайлова автоматической системы 4-го порядка

Рис. Годограф Михайлова автоматической системы 4-го порядка

Решение:
Поскольку годограф Михайлова для заданной автоматической системы проходит последовательно 4 квадранта плоскости XY, при изменении угловой частоты от 0 до ∞, то система является устойчивой [2, ст. 146]. Количество прохождений квадрантов должно быть равно порядку системы. В заданном случае – 4.

Если данная работа оказалась полезной для вас, то мы были бы признательны вам за небольшую финансовую поддержку нашего проекта http://www.zachet.ru/donate/

ПЕРЕЧЕНЬ ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Атабеков Г. И. Основы теории цепей. Учебник для вузов. М., «Энергия», 1969. 424 с. с илл.
2. Теория автоматического регулирования. Бесекерский В. А., Попов Е. П., издательство «Наука», Главная редакция физико-математической литературы, М., 1972, 768 стр.
3. Беседы по автоматике. Голубничий Н. И., Зайцев Г. Ф., Иващенко М. А., Чинаев П. И., Чумаков Н. М. «Техника», 1971, 232 стр.

Максим 25 июля, 2015

Posted In: 2. Критерий устойчивости Михайлова, 3. Устойчивость линейных систем, Задача, Пример решения, Сборник задач по теории автоматического регулирования и управления под редакцией В.А.Бесекерского, ТАУ

Задача 123 по ТАУ, Бесекерский В.А.

Задача 134 по ТАУ, Бесекерский В.А.

Задача 125 по ТАУ, Бесекерский В.А.

Задача № 130 по ТАУ, В.А. Бесекерский

Задача № 120 по ТАУ, В.А. Бесекерский