Дискретная математика

Задача 1. Используя правила де Моргана, получить ДНФ и упростить ее: $x\cdot \overline{x\overline{z}\vee y\overline{z}}$ .

Задача 11. Даны две функции: $f_{1}\left ( x,y \right ) = x + \left ( x\rightarrow y \right )$ , $f_{2}\left ( x,y,z \right ) = \left ( x \sim y \right )\downarrow\overline{x}z$ . Требуется:
а) для функции f₁(x,y) составить таблицу истинности и найти по ней полином Жегалкина, СДНФ, СКНФ. Упростить, если возможно, СДНФ;
б) для функции f₂(x,y,z) составить таблицу истинности и найти по ней полином Жегалкина, СДНФ, СКНФ. По карте Карно получить минимальную ДНФ, нарисовать эквивалентную РКС;
в) составить таблицу Поста для системы функций f₁(x,y), f₂(x,y,z), проверить полноту системы и выбрать базисы, если она полная.

Задача 21. Составить для данного графа структурную матрицу. Найти: а) все простые пути из вершины i=3 в вершину j=1; б) совокупность всех сечений между вершинами i и j.

M2261_6

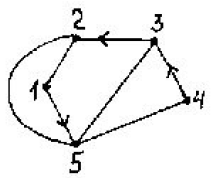
Задача 31. Заданы сеть и начальный поток f:

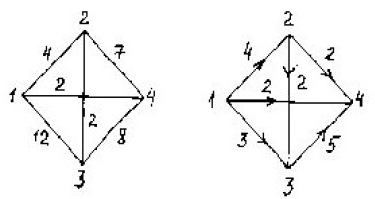
Требуется построить максимальный поток, считая вершину с номером 1 источником и вершину с номером 4 стоком. Указать минимальное сечение, величина которого равна максимальному потоку.

Задача 41. На множестве A={1,2,3,4,5,6} задано отношение делимости: xRy тогда и только тогда, когда x делится на y. Для каждого отношения нужно:
а) записать отношение R;
б) построить матрицу смежности и граф отношения;
в) проверить, является ли отношение рефлексивным, симметричным, транзитивным.

(далее…)

Максим 25 августа, 2014

Posted In: Дискретная математика, Контрольная работа, Математика

Задача 2. Привести данные выражения к ДНФ, пользуясь правилами де Моргана. Если возможно, сократить ДНФ, используя свойство поглощения и правило Блейка:

Задача 12.а) Написать по данной ДНФ полином Жегалкина, от ДНФ перейти к КНФ, а затем перейти к СКНФ; б) перейти от данной КНФ к ДНФ, а затем перейти к СДНФ.

Задача 22.Составить таблицу истинности данной функции, написать для нее СДНФ и СКНФ (если возможно); найти по таблице истинности полином Жегалкина для данной функции; составить карту Карно для данной функции и найти сокращенную ДНФ.